Generating Playable Marupeke Puzzles: Finding Fun in Random Gaps

Last month I finally reached a point in my puzzle generation code where it’s now possible to generate complete and valid puzzle grids.

If you missed my previous post, I shared examples of some earlier generated puzzles.

Censorship and Marupeke

The temperature is finally increasing, spring is almost here. This means I can start some consciousness expanding projects that I have been putting off due to low ambient temperatures. I have generously received a Panaeolus cyanescens spore from a supplier and would like to cultivate the psychedelic mushroom here in

popadoGiovanni Martina

Now, the next step is to make those puzzles playable. Here’s the basic algorithm I used.

1. 10,000 Attempts: The algorithm tries up to 10,000 times to generate a single puzzle. Since we’re working with random puzzles, many don’t pass the final evaluation to be considered interesting, so we re-try the process.
2. Filling the Board: First, the algorithm fills the entire board, a 2D grid represented by the type Vec<Vec<Cell>>. This filled grid is a complete puzzle, ready to be worked on.
3. Removing Cells: The filled grid is passed to the remove_candidates function, which randomly selects cells to remove. After each removal, the function checks whether the puzzle remains solvable.
4. Evaluating the Result: We use the area_filled function to calculate how much of the grid is occupied by crosses or circles. If the filled area is small enough, we’ve found an engaging puzzle. Surprisingly, many generated puzzles have too many filled cells, leaving few interesting moves for the player to explore.

Removing cells

Once the puzzle is fully filled, the next challenge is to remove cells to make it playable and engaging. A good puzzle should have enough empty cells to give players room to make meaningful decisions and progress, keeping it both challenging and enjoyable.

This process itself is a loop where we keep removing cells while not stuck.

The idea here is to keep track of how many removable cells (those with either a cross or a circle) we have, randomly try to remove one, check if the puzzle is solvable and abort the loop when we got stuck on the same number of candidates for a long time.

Since cell removal is random, if the number of removable candidates stays the same for a long time, it’s likely we’ve tried all options without success. At that point, we stop the process and evaluate the board to decide if it qualifies as a “good” puzzle.

This process is still slow since everything runs sequentially for now. But I already have ideas for speeding it up by adding concurrency to the Rust code, maybe in the next iteration.

Here’s a screen recording of successful generations in different tmux panes and a closer look at one of the generated puzzles.

The following output indicates the starting board and final playable puzzle.

Board:
|X|O|X|O|
|O|O|X|O|
|X|X|O|X|
|O|X|X|B|

Num candidates: 4
Count: {11: 1, 4: 2500, 7: 3, 13: 1, 12: 2, 15: 1, 9: 1, 8: 1, 14: 1, 6: 3, 10: 2, 5: 10}
Area: 0.25

| | | | |
| |O| |O|
| |X| | |
| | |X|B|

Let’s play it and see if it’s actually valid.

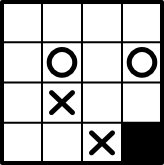
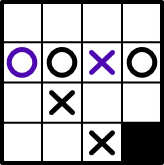
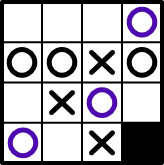
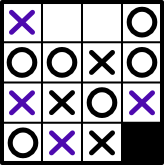
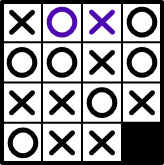
As you can see we end up back with the same original board.

What’s Next?

For now, the algorithm generates puzzles through trial and error, but there’s still room for optimization both in terms of speed and puzzle quality. Next up, I plan to refine the code further, maybe experiment with concurrency, and share some playable puzzles on marupeke.today.

Stay tuned for more updates, and maybe give one of these puzzles a try yourself once they’re live.